Social Force Model
Introduction to Social Force Model
The Social Force Model [1] is a force-based model that defines the movement of pedestrians by the combination of different social forces affecting an individual.
The model defines forces that affect an individual:
- A driving force
- A repulsive force
- An obstacle force
The driving force represents a person’s desire to move in a certain direction, independent of other people and obstacles. The repulsive force is caused by the interaction between the individuals and causes them to avoid each other in order to avoid collisions. The obstacle force acts in a similar way to the person force to avoid collisions with obstacles in the environment.
Driving force
The driving force defines the force that propels pedestrians towards their intended destinations:
$$ \overrightarrow{F_i^{\mathrm{drv}}}=\frac{v_i^0\overrightarrow{e_i^0} - \overrightarrow{v_i}}{\tau}$$
- $v_i^0$ is the desired speed
- $\overrightarrow{e_i^0}$ is the desired direction
- $\overrightarrow{v_i}$ is the currect velocity
- $\tau$ is the reaction time
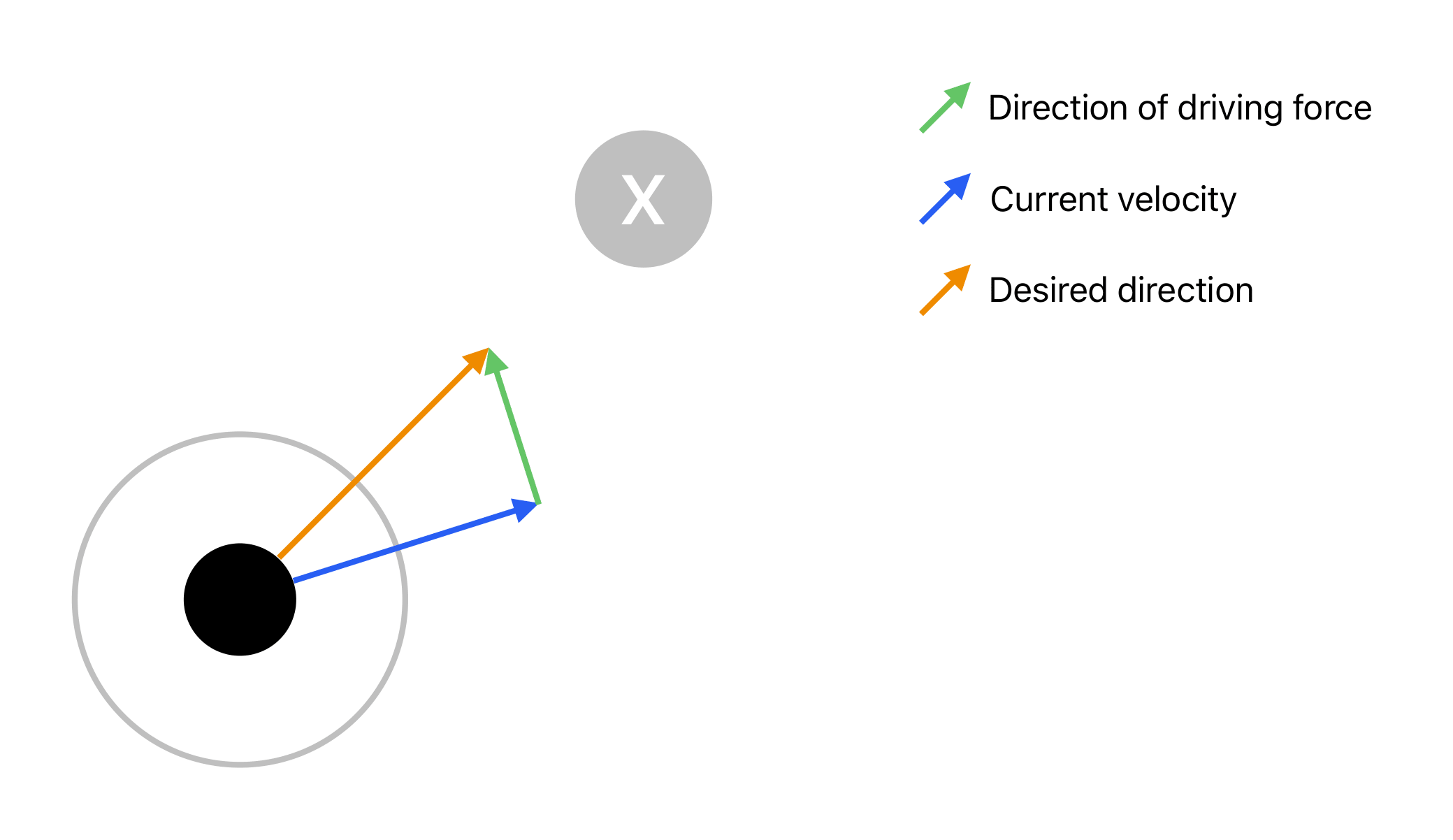
Driving Force acting on an agent.
In the figure above, the black dot represents an agent. Its radius is represented by the gray circle around it. The desired velocity ($v_i^0 \overrightarrow{e_i^0}$) is as big as its desired speed and is pointing in the desired direction towards a destination indicated by an X. The driving force of the agent results from the difference between the desired velocity and the current velocity divided by $\tau$.
Repulsive force
Agents exert an exponentially increasing repulsive force on each other as their proximity decreases. Upon collision, not only do the pushing forces intensify further, but a frictional force also arises. This frictional force acts perpendicularly to the repulsive force, aligning with the direction of the difference in speed
$$ \overrightarrow{F_i^{\mathrm{rep}}} = \sum_{j} \overrightarrow{f_{ij}}\text{.}$$
$$\overrightarrow{f_{ij}} = [A_i \exp[(r_{ij} - d_{ij})/B_i] + kg(r_{ij} - d_{ij})] \overrightarrow{n_{ij}} + \kappa g(r_{ij} - d_{ij}) \Delta v_{ji}^t \overrightarrow{t_{ij}} \text{.}$$
$$\phantom{……}\fbox{\phantom{……………..} pushing \phantom{……………..}} \fbox{\phantom{……} sliding \phantom{……}}$$
- $j$ is another agent
- $r_{ij} = r_i + r_j$ is the combined radius of $i$ and $j$
- $d_{ij}$ is the distance between $i$ and $j$
- $A_i$, $B_i$, $k$ and $\kappa$ are constants (see default values)
- $g$ represents the distance between pedestrians when they are in contact, and is zero when there is no contact. $g(x)~=~\begin{cases} x \text{ if } x > 0 \ \text{ else } 0 \end{cases}$
- $ \overrightarrow{n_{ij}} = (n_{ij}^1, n_{ij}^2) = (\overrightarrow{\mathrm{pos}_i} - \overrightarrow{\mathrm{pos}_j})/d_{ij} $ is the normalised vector from $j$ to $i$
- $ \overrightarrow{t_{ij}} = (- n_{ij}^2, n_{ij}^1)$ is the tangent of $\overrightarrow{n_{ij}}$ which is perpendicular to it, rotated counterclockwise
- $\Delta v_{ji}^t = (\overrightarrow{v_j} - \overrightarrow{v_i}) \cdot \overrightarrow{t_{ij}}$ is the tangential velocity difference of $i$ and $j$
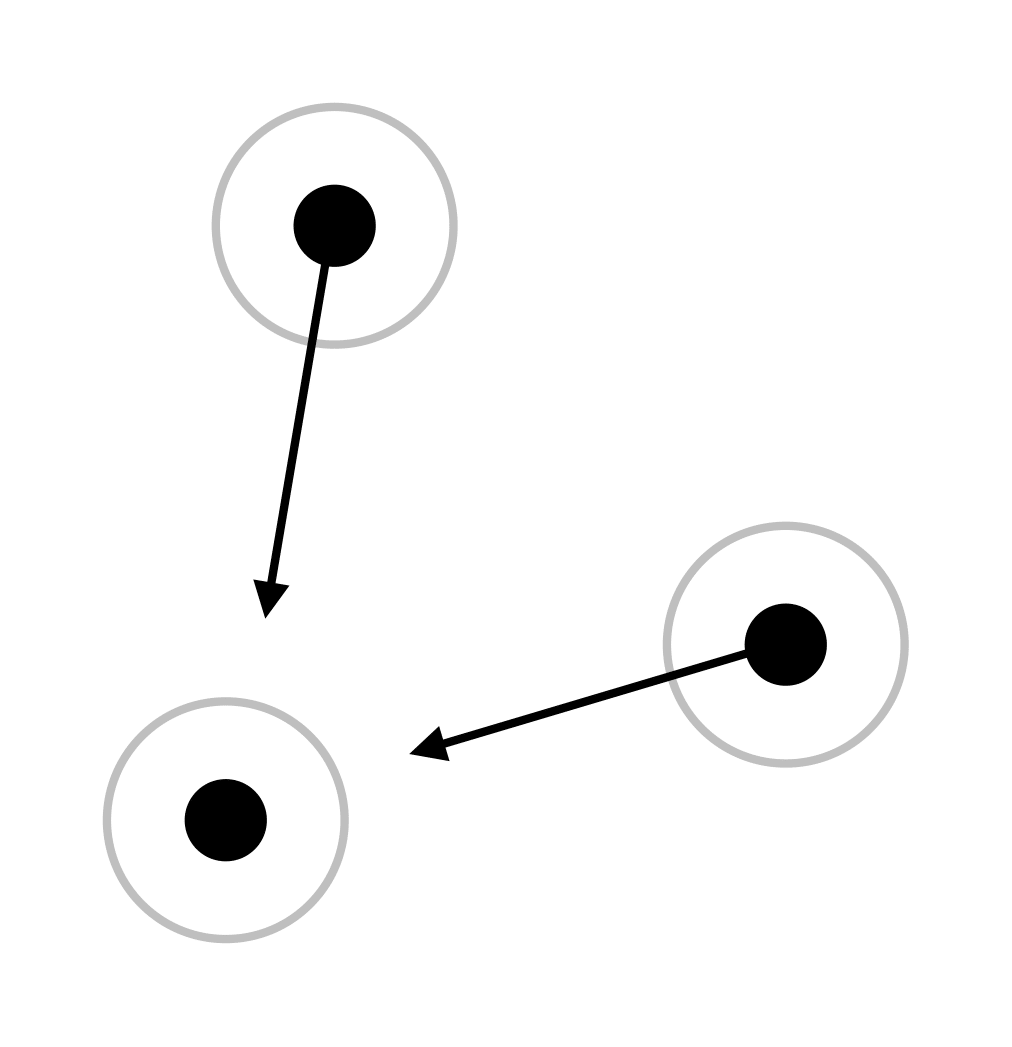
Direction of repulsive forces acting on an agent.
The repulsive force of the agents acts from the originating agent towards the agent on which the forces act. When their distance greater than their combined radius no other forces apply.
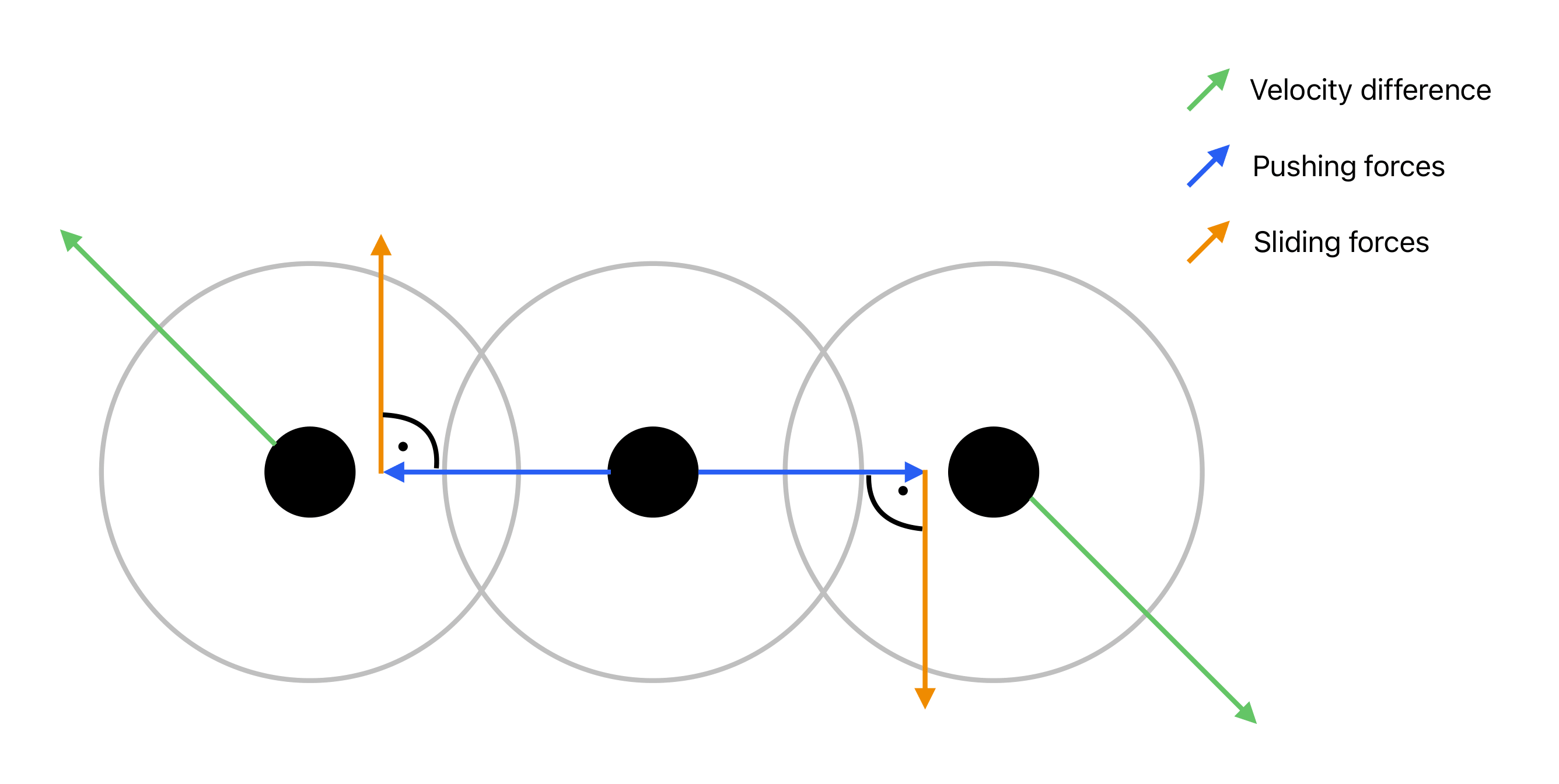
Direction of the pushing and frictional forces acting on colliding agents.
If the distance between two agents is smaller than their combined radius, the agents collide and a frictional force also occurs. This frictional force acts orthogonally to the repulsive force in the direction of the velocity difference of the two agents.
Obstacle force
Obstacles exert a force on the agent similar to a static agent. Each line segment of an obstacle exerts force on the agent. The repulsive force is increases exponentially with decreasing distance. When the agent collides with the segment the repulsive forces are increased additionally. When colliding, a frictional force also occurs, which acts orthogonally to the repulsive force in the direction to the velocity of the agent
$$ \overrightarrow{F_i^{\mathrm{obst}}} = \sum_{o} \overrightarrow{f_{io}\text{.}}$$
$$\overrightarrow{f_{io}} = [A_i \exp[(r_{i} - d_{io})/B_i] + kg(r_{i} - d_{io})] \overrightarrow{n_{io}} + \kappa g(r_{i} - d_{io}) (\overrightarrow{v_{i}}\cdot\overrightarrow{t_{io}}) \overrightarrow{t_{io}} \text{.}$$
$$\phantom{………}\fbox{\phantom{………………} pushing \phantom{……………..}} \fbox{\phantom{……….} sliding \phantom{……….}}$$
- $o$ is a segment of the obstacle
- $r_i$ is the radius agent $i$
- $d_{io}$ is distance from closest point on the segement to $i$
- $\overrightarrow{n_{io}} = (n_{io}^1, n_{io}^2) = (\overrightarrow{\mathrm{pos}_i} - \overrightarrow{\mathrm{pos}_o})/d_{io}$ the direction from $\overrightarrow{\mathrm{pos}_o}$ the closest point on the segment to $i$
- $ \overrightarrow{t_{io}} = (- n_{io}^2, n_{io}^1)$ is the tangent of $\overrightarrow{n_{io}}$ which is perpendicular to it, rotated counterclockwise
- $v_i$ is the velocity of $i$
- $A_i$, $B_i$, $k$ and $\kappa$ are constants (see default values)
- $g$ represents the distance between a pedestrian and an obstacle segment when they are in contact, and is zero when there is no contact. $g(x)~=~\begin{cases} x \text{ if } x > 0 \ \text{ else } 0 \end{cases}$
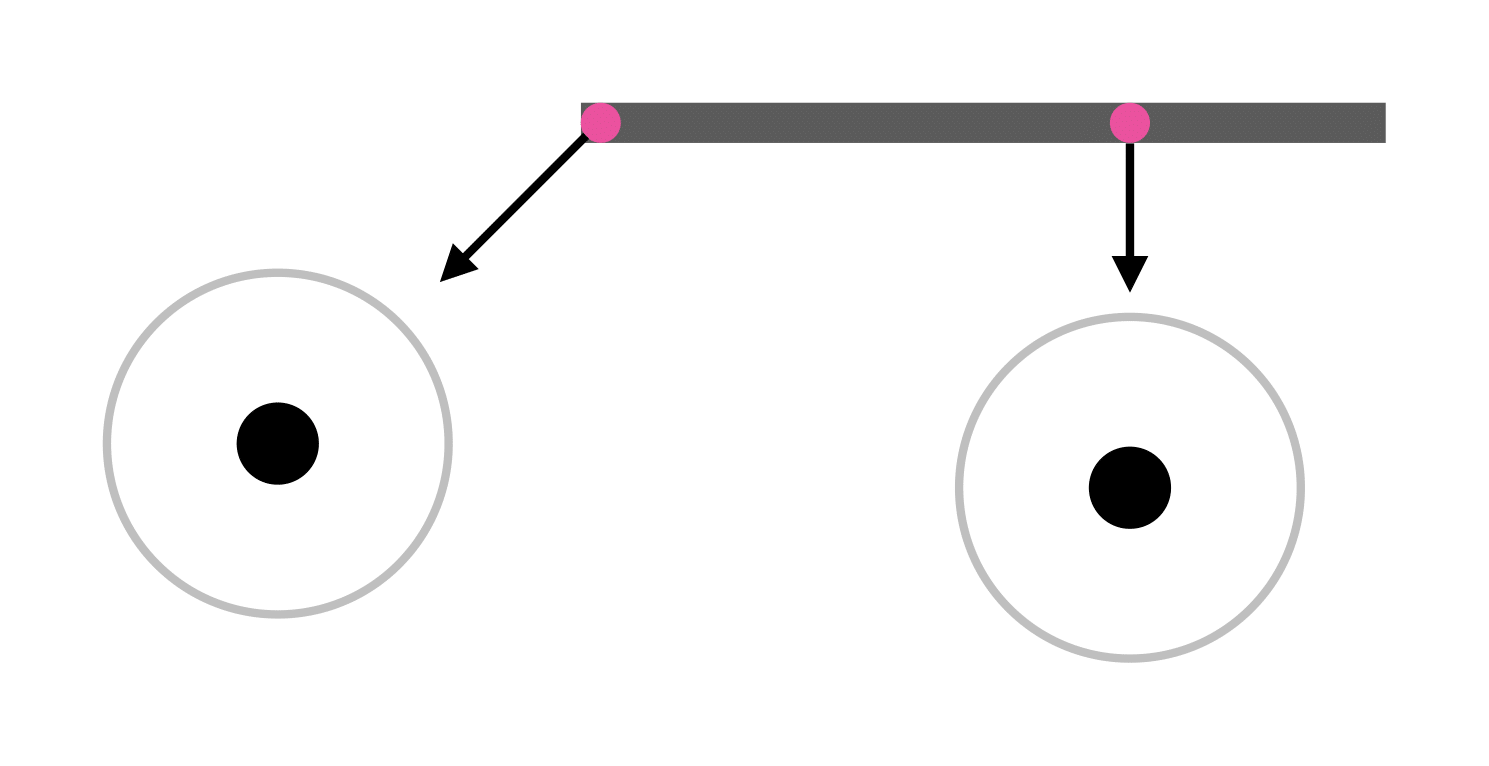
Direction of repulsive forces acting on an agent.
the repulsive force originating from a segment of an obstacle acts from the point on the wall segment that is closest to the agent. This point is marked in magenta in the illustration above.
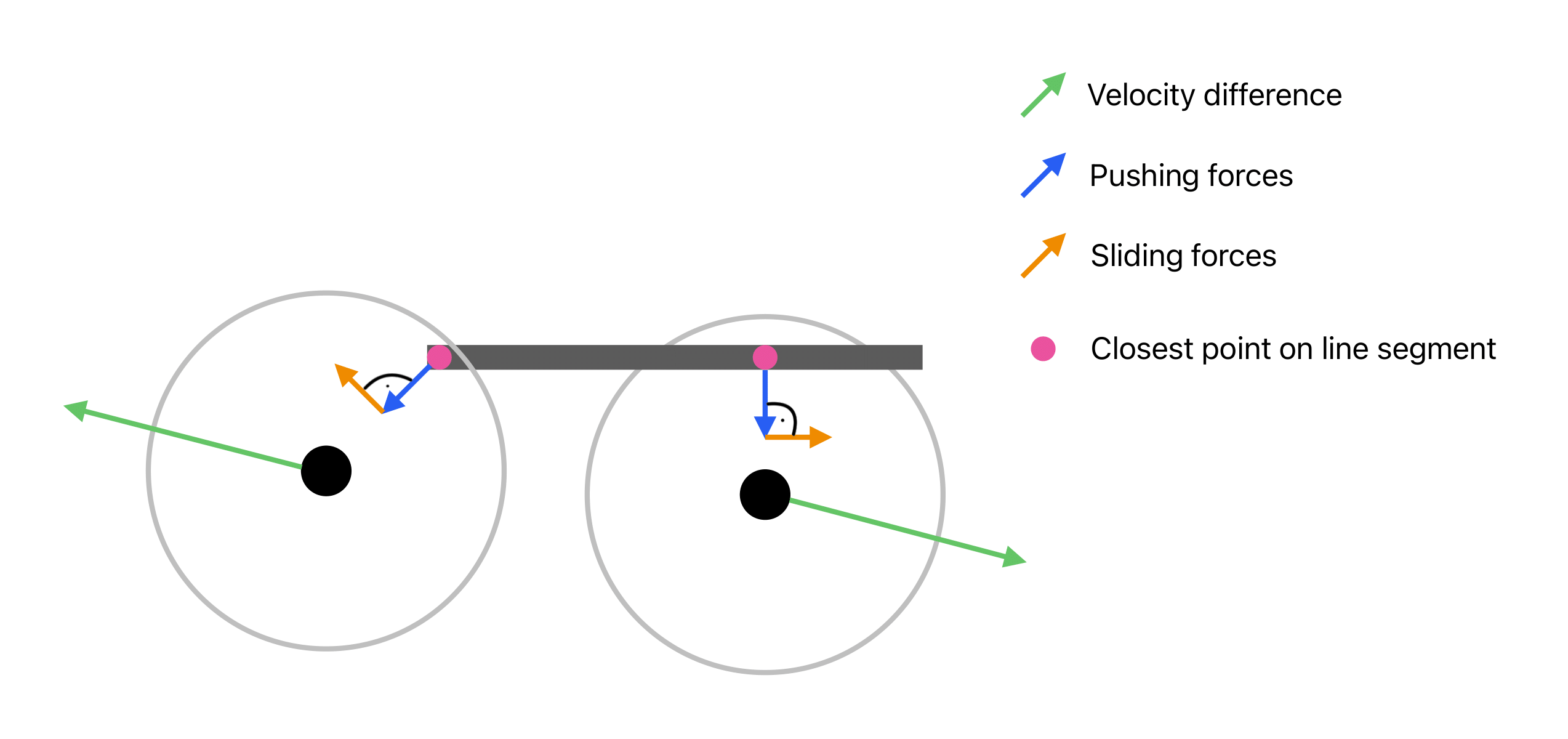
Direction of the pushing and frictional forces acting on agents colliding with an obstacle segment.
When the minimum distance between an agent and a wall segment falls below the agent’s radius, an additional frictional force comes into effect. This frictional force acts orthogonally to the repulsive force in the direction of the velocity of the agent.
Calculating new velocity and new position from forces
With the definition of the forces affecting an individual, it is possible to calculate its new speed
$$ \overrightarrow{v_{\mathrm{new}}} = \overrightarrow{v_i} + [\overrightarrow{F_i^{\mathrm{drv}}} + \frac{\overrightarrow{F_i^{\mathrm{rep}}} + \overrightarrow{F_i^{\mathrm{obst}}}}{m_i}] \cdot \delta T$$ and position $$ \overrightarrow{\mathrm{pos}_{\mathrm{new}}} = \overrightarrow{\mathrm{pos}_i} + \overrightarrow{v_{\mathrm{new}}} \cdot \delta T \text{.}$$
Here $m_i$ denotes the mass of $i$ and $\delta T$ denotes the length one simulation iteration.
Default values
| Parameter | Value | Unit |
|---|---|---|
| $A_i$ | 2_000 | N |
| $B_i$ | 0.08 | m |
| $k$ | 120_000 | $\mathrm{\frac{kg}{s^2}}$ |
| $\kappa$ | 240_000 | $\mathrm{\frac{kg}{m \cdot s}}$ |
| $r_i$ | 0.3 | m |
| $\tau$ | 0.5 | s |
| $v_i^0$ | 0.8 | $\mathrm{\frac{m}{s}}$ |
| $m$ | 80 | kg |
References
- [1] Helbing, D., Farkas, I., Vicsek, T. (2000).
Simulating dynamical features of escape panic. In: Nature
https://doi.org/10.1038/35035023