Optimal Steps Model
Introduction
The basic idea of the Optimal Steps Model (OSM) is that virtual pedestrians (agents) try to improve their situation with every step. The utility of each position in space is coded in a scalar function called floor field. Utility increases when approaching targets and decreases when getting too close to obstacles and other virtual pedestrians. From a physical perspective, agents in motion are drawn towards targets while being repelled by obstacles and other agents. In other words, the negative utility can be understood as a potential that agents aim to minimize. The utility, or potential, depends on the geodesic distance to the target and the proximity to other agents.
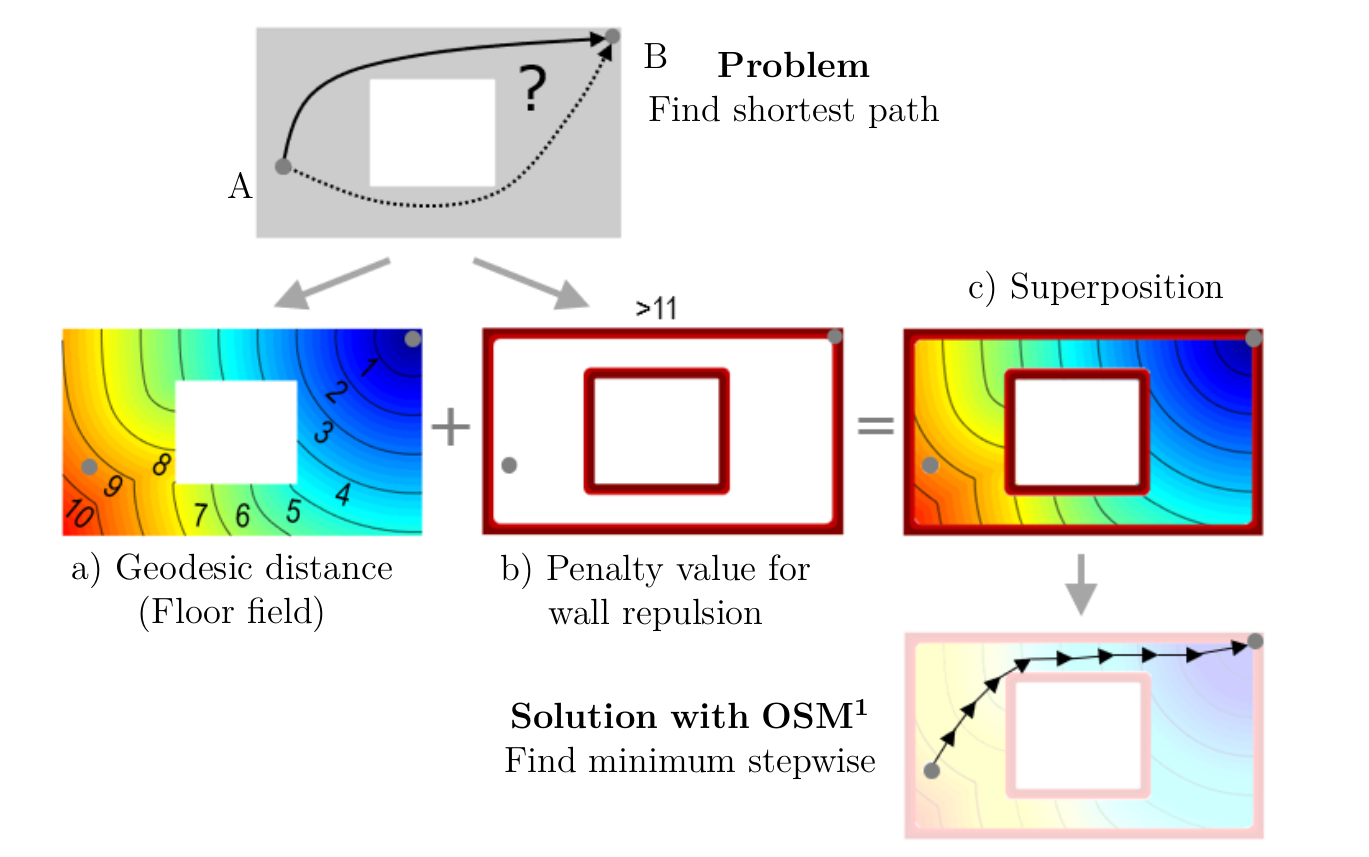
Schematic solution of routing with OSM. Master thesis C. Mayr: The Heat Method for geodesic distance computation on 2D domains
Agents move by stepping on the position on a circle (or disk) around their current location that optimizes this utility. The circle radius represents each agent’s personal maximum stride length, which in turn is linearly correlated to the agent’s free-flow speed [1], that is, an assumed desired speed when the path is free. Thus, agents step toward targets while skirting obstacles and avoiding collisions. For the remainder of the text and in the figures, we adopt the physical interpretation consistent with the parameter names in Vadere’s implementation of the OSM.
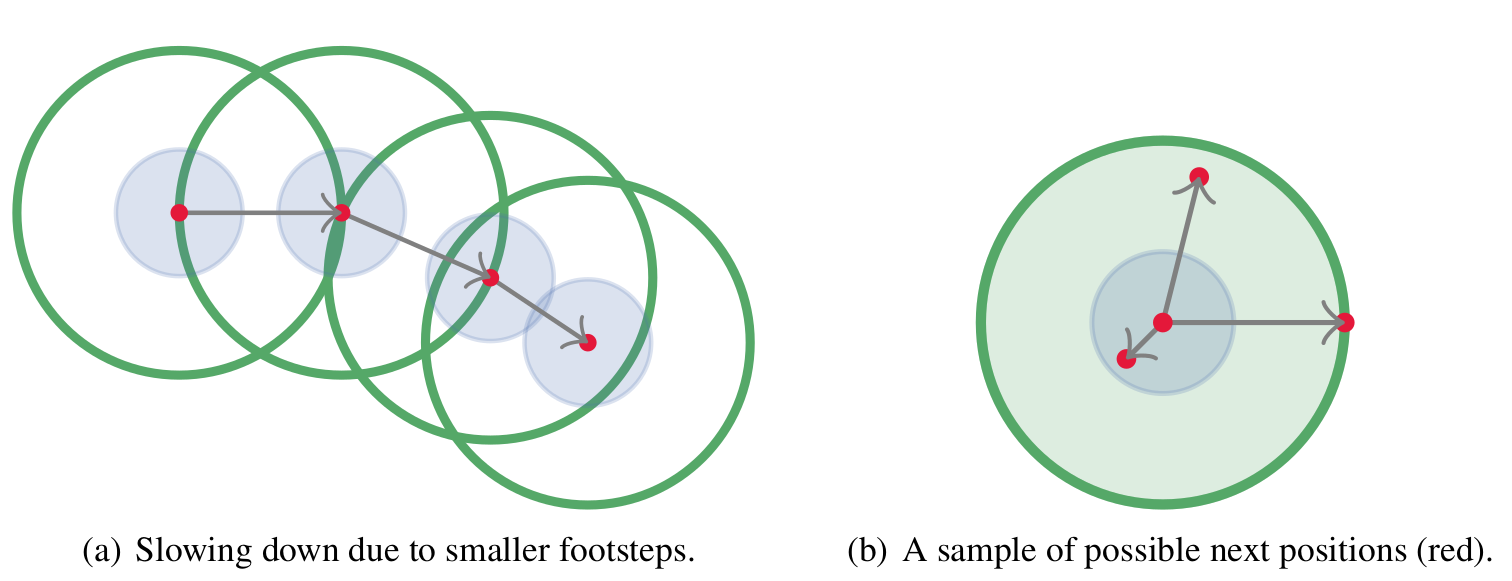
Modeling steps with OSM.
Mathematical description
The potential $P_l(x)$ for pedestrian $l$ at time $t$ for an arbitrary point $x \in \mathbb{R}^2$ in the plane is defined as [1]
$$ P_l(x) = P_t(x,s) + \sum_{j=1}^m P_{o,j}(x) + \sum_{i=1,i\neq l}^n P_{p,i}(x), $$
where $P_t(x,s)$ is the attraction potential of the target, $s$ is the vector of the current agent positions, $P_{o,j}(x)$ is the repulsive potential induced by obstacle $j$, $m$ is the number of obstacles, $P_{p,i}$ is the repulsive potential of other agents, $n$ is the number of agents. The implementation of the attraction potential $P_t(x)$ is the so-called floor field. If the attraction potential does not depend on the agents’ current positions, means $P_t(x,s)=P_t(x)$, the floor field is static. Otherwise, it is dynamic. If we consider the floor field to be static, the value of the potential function at position $x$ equals the negative geodesic distance between $x$ and the target.
The obstacle potential $P_{o,j}(x)$ is defined as
$$ P_{o,j}(x) = \begin{array}{ll} \delta_1(x) + \delta_2(x) & d_{o,j}(x) < r_l \\ \delta_1(x) & r_l \leq d_{o,j}(x) < w_o \\ 0 & \textrm{otherwise,} \\ \end{array} $$ where $d_{o,j}(x)$ is the Euclidean distance to the closest point of the obstacle from position $x$, $w_o$ defines the width of the obstacle repulsion, $r_l$ is the torso radius of agent $l$. The functions $\delta_i$ are defined as $$ \begin{align} \delta_1(x) &= 6 \exp{\left[ 2 \left( \left( \frac{d_{o,j}(x)} {w_o} \right)^{2} - 1\right)^{-1} \right]};\text{and}\\ \delta_2(x) &= 10^5 \exp{\left[ \left( \left( \frac{d_{o,j}(x)} {r_l} \right)^{2} - 1\right)^{-1} \right]}. \ \end{align} $$ The repulsion between two agents is achieved by the distance-dependent potential function $P_{p,i}$. In Vadere, it is implemented as
$$ P_{p,i}(x) = \begin{array}{ll} \phi_1(d_{l,i}(x)) + \phi_2(d_{l,i}(x)) + \phi_3(d_{l,i}(x)) & d_{l,i}(x) <r_i + r_l, \\ \phi_1(d_{l,i}(x)) + \phi_2(d_{l,i}(x)) & r_i + r_l \leq d_{l,i}(x) < w_{int} +r_i+r_l, \\ \phi_1(d_{l,i}(x)) & w_{int} + r_i + r_l \leq d_{l,i}(x) < w+r_i+r_l\\ 0, & \textrm{otherwise,} \\ \end{array} $$
where $d_{l,i}(x)$ is the Euclidean distance between agent $l$ and agent $i$. $r_i, r_l$ are the respective torso radii of agent $i,l$. $w_{int}$ and $w$ are the intimate and the personal space width according to Hall. The functions $\phi_i$ are defined as $$ \begin{align} \phi_1({d_{i,j}}) &= \mu \exp{\left[ 4 \left( \left( \frac{d_{i,j}} {w +r_i +r_l} \right)^{2} - 1\right)^{-1} \right]} \\ \phi_2({d_{i,j}}) &= \frac{ \mu } {a_p} \exp{\left[ 4 \left( \left( \frac{d_{i,j}} {w_{int} +r_i +r_l} \right)^{2} - 1\right)^{-1} \right]} \\ \phi_3({d_{i,j}}) &= 10^3 \exp{\left[ \left( \left( \frac{d_{i,j}} {r_i +r_l} \right)^{2} - 1\right)^{-1} \right]} \end{align} $$
The potential function is based on Hall’s theory of interpersonal distances which describes four distance zones around a person [4]. Accordingly, the potential function is defined piece-wise on rings around each agent: a circular core for collision avoidance, a first ring that represents the intimate space, and a second ring that represents personal space. Agents outside the personal zone do not affect other agents’ path choice. This is mathematically modeled by setting the the potential function to zero.
![Agent’s potential versus distance for different parameter values. [5]](figure3.png)
Agent’s potential versus distance for different parameter values. [5]
The value of the potential function in the personal space ring is very low. Thus, this area will be kept free only if agents have ample space to avoid each other [3]. As soon as the space becomes more constricted agents will get closer. This is typical for normal human behavior. In the intimate space ring, the potential function value increases significantly. In crowds, this area is only kept free if the density is low [3]. Finally, to prevent agents from overlapping, the potential is set to a high value (compared to the values for the personal and intimate spaces) in the collision area. The exact definition of the potential function and default parameters implemented in Vadere can be found in [2].
Implementation in Vadere, Challenges, Limitations, Usage, Parameters
Vadere simulator
The Vadere project was started in 2010. Its main intention was and still is to facilitate development and comparison of locomotion models. Therefore, it was designed as a generic framework, but with an eye on keeping it lightweight, so that new locomotion models can be quickly implemented. Vadere has an event-driven update scheme and a simulation loop.

Vadere simulation loop.
The Optimal Steps Model implements the locomotion model interface Model that contains four essential methods:
initialize(): compute floorfield, initialize step circle optimizer and update scheme.preLoop(): set last time step.postLoop(): shut down update scheme.update(): set new time step and solve optimization problem to find the next position.
Usage
Vadere is implemented in Java programming language. Thus, it is available for GNU-/Linux, MacOS and Microsoft Windows. Vadere reads in simulation parameters, like the topography or an agent’s radius, from a human-readable JSON-based text file instead of using a binary format. Also, the simulation results — usually x and y coordinates for each pedestrian and a time step — are written to text files. In this way, users can use text editors to create input files for Vadere and they can open result files from Vadere with 3rd-party software like MATLAB. Furthermore, text files allow users to modify parameters quickly in an automated way. This is essential for studies where parameters must be varied and, thus, thousands of simulations must be run. Performing simulations with Vadere requires three steps. These steps are supported by the graphical user interface.
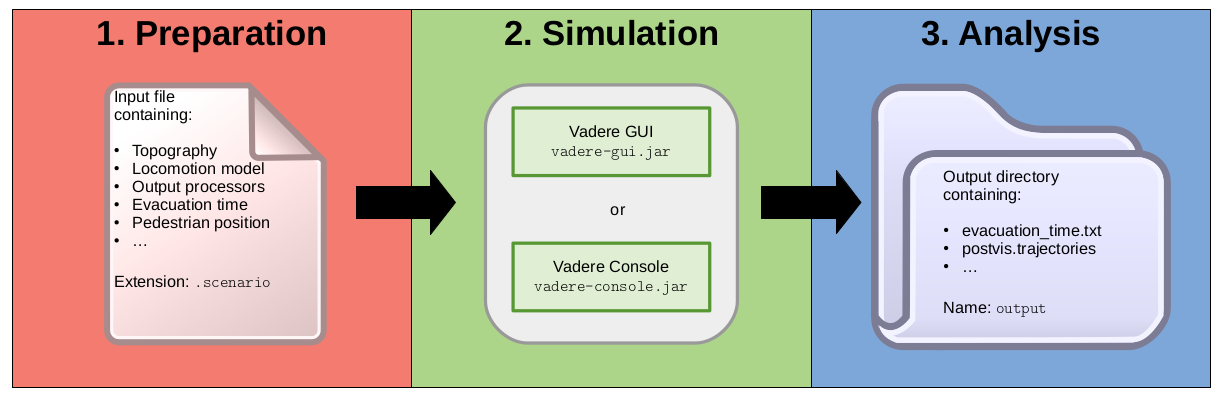
Vadere interface.
Challenges and limitations
Using the OSM involves solving many optimization problems. For each step of each agent, a non-trivial optimization problem has to be solved. This optimization is computationally expensive and requires most of the overall computation time. Introducing more complex potential functions complicates the evaluation of the potential function which contributes directly to the computation time of the optimization. Evaluating the potential function at specific points only instead of using an optimization technique such as Nelder Mead can accelerate the simulation. Note that when you cut down the number of evaluation points to 8, this will mimic a cellular automaton.
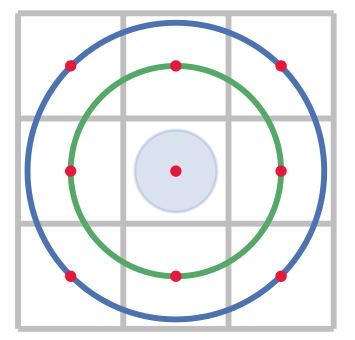
Grid discrimination.
This is aggravated by the fact that a strict event-driven update hinders parallelization of the computation. Therefore, simulating thousands of agents in real-time using the OSM with Vadere is not yet possible. Benedikt Zönnchen worked on the acceleration in his dissertation thesis.
Parameters
The shape of the potential function is controlled through several parameters. There are two parameters that are especially important for the distancing behavior which is why we introduce them briefly:
- the potential height $h$ (in Vadere:
pedPotentialHeight) - and the personal space width $w$ (in Vadere:
pedPotentialPersonalSpaceWidth).
The parameter potential height $h$ controls the strength of repulsion. If $h$ is increased, we expect agents to increase their distance to others.
The parameter personal space width $w$ controls how far the repulsion reaches: the larger $w$ the bigger the influence area of an agent. By adusting the personal space width $w$ [5] social distancing can be achieved. Nevertheless, the personal space is related to but not equal to a desired social distance $d$ the user wants to model. When there is ample space, it might suffice to set $w = d$ to keep agents at least the desired social distance apart. Since the true distance between agents is an emergent value, the distance is larger [5].
References
[1] Michael J. Seitz and Gerta Köster. Natural discretization of pedestrian movement in continuous space. Physical Review E, 86(4):046108, 2012.
https://doi.org/10.1103/PhysRevE.86.046108[2] Benedikt Kleinmeier, Benedikt Zönnchen, Marion Gödel, and Gerta Köster. Vadere: An open-source simulation framework to promote interdisciplinary understanding. Collective Dynamics, 4, 2019.
https://doi.org/10.17815/CD.2019.21[3] von Sivers, Isabella Katharina Maximiliana. Modellierung sozialpsychologischer Faktoren in Personenstromsimulationen. Dissertation Technical University Munich, 2016.
[4] Edward Twitchell Hall. The Hidden Dimension. Doubleday, New York, 1966.
[5] Christina M. Mayr and Gerta Köster. Social distancing with the Optimal Steps Model. Collective Dynamics, 2021.
https://doi.org/10.17815/CD.2021.116[5] Xu, Q., Chraibi, M., Seyfried, A. (2021). Anticipation in a velocity-based model for pedestrian dynamics. Transportation Research Part C: Emerging Technologies, Volume 133.